Page 85 - Guide du Dessinateur Industriel

20.4 T1.oisième exemple @An--

Soit à établir pour l'ensemble ci-contre, la chaîne
minimale des cotes permettant l'immobilisation en
translation des pièces 3b, 4, 5, 7 et 3a sur l'arbre 2
à l'aide de I'anneau élastique 8.

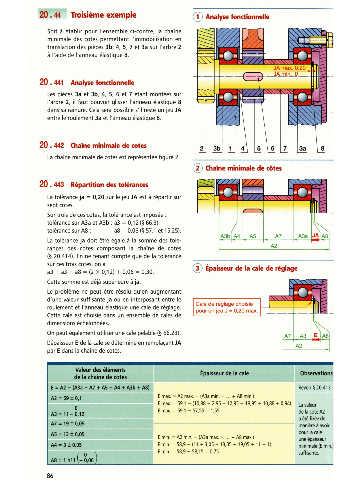
20.441 AnwfonctioMclle
Les pièces 3a et 3b, 4, 5, 6 et 7 étant montées sur
l'arbre 2, il faut pouvoir glisser I'anneau élastique 8
dans sa rainure. Cela sera possible s'il reste un jeu JA
entre le roulement 3a et I'anneau élastique 8.

20.442 Chahminimaiadamtes
La chaîne minimale de cotes est représentée figure 2.

20 ,443 Ripartition des tohnœs

La tolérance ja = 0,20 sur le jeu JA est à répartir sur
sept cotes.
Sur trois de ces cotes, la tolérance est imposée :
tolérance sur A3a et A3b : a3 = 0,12 (5 66.3)
tolérance sur A8 : a8 = 0,06 (5 57.1 et 15.25).
La tolérance ja doit être égale à la somme des tolé-
rances des cotes composant la chaîne de cotes
(5 20.414). En ne tenant compte que de la tolérance
sur ces trois cotes, on a :
a3 + a3 + a8 = (2 x 0,12) + 0,06 = 0,30.
Cette somme est déjà supérieure à ja.
Le problème ne peut être résolu qu'en augmentant
d'une valeur suffisante ja ou en interposant entre le
roulement et I'anneau élastique une cale de réglage.
Cette cale est choisie dans un ensemble de cales de
dimensions échelonnées.
On peut également utiliser une cale pelable (5 66.23).
L'épaisseur E de la cale se détermine en remplaçant JA
par E dans la chaîne de cotes.

1 de la chaine de des
Valeur des éléments

E max. = Aî max. - (A3a min. + ... + AS min.)
E mw. = 59.1 - (IO,@ + 2,s + 12,% + 18,s + 10.88 + 034)
1 E ma. = 59,l - 57,55 = 1,55
- - -. I
it
8 -
Emm.=AZmin .- Wamax.+ ...+ Mm)
E min. = 5&9 - (11 + 3.05 + 13.05 + 19,05 t 11 + 1)
E min. = 58,9 - 58,15 = a75